Joint pdf of a uniform distribution West Coast

The Joint PDF of Two Uniform Distributions Physics Forums 1/29/2017В В· Learn to use pictures to solve problems involving Joint Uniform distributions. Joint Uniform Distribution Mancinelli's Math Lab. Joint Probability Distributions for Continuous Random

Joint Distribution of Two Uniform Random SpringerLink

Theorem Proof X1 X U Y X William & Mary Mathematics. Schaum's Outline of Probability and Statistics 36 CHAPTER 2 Random Variables and Probability Distributions (b) The graph of F(x) is shown in Fig. 2-1. The following things about the above distribution function, which are true in general, should be noted., That is, the conditional PDF of \(Y\) given \(X\) is the joint PDF of \(X\) and \(Y\) divided by the marginal PDF of \(X\). It’s now clear why we discuss conditional distributions after discussing joint distributions: we need joint distributions to calculate the conditional distribution (the joint PDF is in the numerator!)..

Answer to: Let X have a uniform distribution over (0, 2) and the conditional distribution of y given X = x, be uniform distribution over [0, x^2]. 4. Joint Distributions Basic Theory Thus, by definition, the joint probability density function of (X, Y) is The following exercise shows how an arbitrary continuous distribution can be obtained from a uniform distribution. This result is useful for simulating certain continuous distributions.

1.4 Conditional Distribution of Order Statistics In the following two theorems, we relate the conditional distribution of order statistics (con-ditioned on another order statistic) to the distribution of order statistics from a population whose distribution is a truncated form of the original population distribution function F(x). Theorem 2 Let 2.3.2 Joint Distribution of Two or More Order Statistics . . . . . . . . .19 3 Order Statistics from Uniform Distribution 61 from a population having a continuous probability density function. Tippett (1925) extended the work of Pearson and found the mean value of the sample

6 Jointly continuous random variables Again, we deviate from the order in the book for this chapter, so the subsec-tions in this chapter do not correspond to those in the text. 6.1 Joint density functions Recall that X is continuous if there is a function f(x) (the density) such that P(X ≤ t) = Z t −∞ f X(x)dx 2.3.2 Joint Distribution of Two or More Order Statistics . . . . . . . . .19 3 Order Statistics from Uniform Distribution 61 from a population having a continuous probability density function. Tippett (1925) extended the work of Pearson and found the mean value of the sample

2.3.2 Joint Distribution of Two or More Order Statistics . . . . . . . . .19 3 Order Statistics from Uniform Distribution 61 from a population having a continuous probability density function. Tippett (1925) extended the work of Pearson and found the mean value of the sample 1 Order Statistics Definition The order statistics of a random sample X1, (Uniform order statistics pdf) The joint pdf of three or more order statistics could be derived using similar but even more involved arguments. Perhaps the other most useful pdf is fX (1),

Problem calculating joint and marginal distribution of two uniform distributions. Ask Question Asked 8 years, 7 months ago. Active 1 year ago. what's the pdf and covariance for this distribution? 5. Problem obtaining a marginal from the joint distribution. 0. In order to compare with the theoretical probability density function (PDF) , I need to simulate the probability density function of random variable. View How can I calculate the joint probability

Theorem The difference of two independent standard uniform random variables has the standard trianglular distribution. Proof Let X1 and X2 be independent U(0,1) random variables. Let Y = X1 −X2. The joint probability density function of X1 and X2 is f X1,X2(x1,x2) = 1 0

1.4 Conditional Distribution of Order Statistics In the following two theorems, we relate the conditional distribution of order statistics (con-ditioned on another order statistic) to the distribution of order statistics from a population whose distribution is a truncated form of the original population distribution function F(x). Theorem 2 Let The joint probability distribution can be expressed either in terms of a joint cumulative distribution function or in terms of a joint probability density function (in the case of continuous variables) or joint probability mass function (in the case of discrete variables).

Lecture 10: Joint Distributions & Order Statistics Sta 111 Colin Rundel May 28, 2014 Joint Distributions Discrete RVs Joint Distribution - Example Draw two socks at random, without replacement, from a drawer full of twelve colored socks: 6 black, 4 white, 2 purple Let B … Joint density problem. Two uniform distributions. Ask Question Asked 5 years, 4 months ago. Find the joint pdf of X and Y for two uniform distributions. 0. Uniform distribution joint density problem. 0. Joint probability density for non-identical Uniform random variables. 0.

The joint probability distribution can be expressed either in terms of a joint cumulative distribution function or in terms of a joint probability density function (in the case of continuous variables) or joint probability mass function (in the case of discrete variables). Lecture 10: Joint Distributions & Order Statistics Sta 111 Colin Rundel May 28, 2014 Joint Distributions Discrete RVs Joint Distribution - Example Draw two socks at random, without replacement, from a drawer full of twelve colored socks: 6 black, 4 white, 2 purple Let B …

The converse does not hold in general. The joint distribution contains much more information than the marginal distributions separately. However, the converse does hold if \(X\) and \(Y\) are independent, as we will show below.. Joint and Marginal Densities Joint PDF of a Uniform Distribution. Ask Question Asked 4 years, 5 months ago. Is the supplied solution just saying that we need all observations to be less than $\theta$ for the joint PDF to yeild something non-trivial? self-study mathematical-statistics uniform. share Marginal of a uniform distribution. 8.

Theorem Proof X1 X U Y X William & Mary Mathematics

4. Joint Distributions MATEMATIKA INTÉZET. It is shown that, in a renewal process with inter-arrival distribution F, an observation from the asymptotic (when t →∞) joint distribution of backward and forward recurrence times at t can be, two distributions are independent if the joint distribution is the same as the product of the two marginal distributions. Miles Osborne (originally: Frank Keller) Formal Modeling in Cognitive Science 19.

Joint PDF of two random variables with Uniform Distribution. In the case of the random sample of size 15 from the uniform distribution on (0;1), the pdf is f X(n)(x) = nx n 1 I (0;1)(x) which is the pdf of the Beta(n;1) distribution. Not surprisingly, all most of the probability or \mass" for the maximum is piled up near the right endpoint of 1. …, In the case of the random sample of size 15 from the uniform distribution on (0;1), the pdf is f X(n)(x) = nx n 1 I (0;1)(x) which is the pdf of the Beta(n;1) distribution. Not surprisingly, all most of the probability or \mass" for the maximum is piled up near the right endpoint of 1. ….

Joint Distribution of Two Uniform Random SpringerLink

Bivariate Distributions University of Washington. Schaum's Outline of Probability and Statistics 36 CHAPTER 2 Random Variables and Probability Distributions (b) The graph of F(x) is shown in Fig. 2-1. The following things about the above distribution function, which are true in general, should be noted. https://fr.wikipedia.org/wiki/Loi_uniforme_continue In the case of the random sample of size 15 from the uniform distribution on (0;1), the pdf is f X(n)(x) = nx n 1 I (0;1)(x) which is the pdf of the Beta(n;1) distribution. Not surprisingly, all most of the probability or \mass" for the maximum is piled up near the right endpoint of 1. ….

The marginal PDF of X is simply 1, since we're equally likely to pick a number from the range of (0,1). We can verify this using calculus by taking the derivative of the CDF, which is simply F(X <= x) = x/1, or x. The derivative of xdx = 1. I'm struggling with the joint PDF. Problem calculating joint and marginal distribution of two uniform distributions. Ask Question Asked 8 years, 7 months ago. Active 1 year ago. what's the pdf and covariance for this distribution? 5. Problem obtaining a marginal from the joint distribution. 0.

4. Joint Distributions Basic Theory Thus, by definition, the joint probability density function of (X, Y) is The following exercise shows how an arbitrary continuous distribution can be obtained from a uniform distribution. This result is useful for simulating certain continuous distributions. In the case of the random sample of size 15 from the uniform distribution on (0;1), the pdf is f X(n)(x) = nx n 1 I (0;1)(x) which is the pdf of the Beta(n;1) distribution. Not surprisingly, all most of the probability or \mass" for the maximum is piled up near the right endpoint of 1. …

Theorem The difference of two independent standard uniform random variables has the standard trianglular distribution. Proof Let X1 and X2 be independent U(0,1) random variables. Let Y = X1 −X2. The joint probability density function of X1 and X2 is f X1,X2(x1,x2) = 1 0

The converse does not hold in general. The joint distribution contains much more information than the marginal distributions separately. However, the converse does hold if \(X\) and \(Y\) are independent, as we will show below.. Joint and Marginal Densities The converse does not hold in general. The joint distribution contains much more information than the marginal distributions separately. However, the converse does hold if \(X\) and \(Y\) are independent, as we will show below.. Joint and Marginal Densities

Joint distributions Math 217 Probability and Statistics The joint probability density function is constantly 1 2 ple was a uniform distribution on a triangle. For this example, we’ll go back to the unit square, but make the distribution nonuniform. We’ll describe of the variables, the joint pmf or pdf of the subset is equal to the product of the marginal pmf’s or pdf’s. 12, ,..., ii i n XX X Slide 12 Stat 110A, UCLA, Ivo Dinov Conditional Probability Function Let X and Y be two continuous rv’s with joint pdf f (x, y) and marginal X pdf f X (x). Then for any X …

An n-dimensional joint uniform distribution is defined as a distribution whose one-dimensional marginals are uniform on some interval I. This interval is taken to be [0,1] or, when more convenient [−1 2, 1 9 2]. The specification of joint uniform distributions 1 Order Statistics Definition The order statistics of a random sample X1, (Uniform order statistics pdf) The joint pdf of three or more order statistics could be derived using similar but even more involved arguments. Perhaps the other most useful pdf is fX (1),

Bivariate Distributions — Continuous Random Variables When there are two continuous random variables, the equivalent of the two-dimensional array is a region of the x–y (cartesian) plane. Above the plane, over the region of interest, is a surface which represents the probability density function associated with a bivariate distribution. In order to compare with the theoretical probability density function (PDF) , I need to simulate the probability density function of random variable. View How can I calculate the joint probability

4. Joint Distributions Basic Theory Thus, by definition, the joint probability density function of (X, Y) is The following exercise shows how an arbitrary continuous distribution can be obtained from a uniform distribution. This result is useful for simulating certain continuous distributions. Solution. Figure 5.8(a) shows $R_{XY}$ in the $x-y$ plane. The figure shows (a) $R_{XY}$ as well as (b) the integration region for finding $P(Y<2X^2)$ for Solved

If I'm understanding the question properly, we want to calculate the pdf of a multivariate uniform distribution. By definition, the pdf is constant for all values in the support the distribution. Thus to calculate the pdf all that is required is to calculate the norming constant, which is given by the inverse of the integral of the support. The converse does not hold in general. The joint distribution contains much more information than the marginal distributions separately. However, the converse does hold if \(X\) and \(Y\) are independent, as we will show below.. Joint and Marginal Densities

That is, the conditional PDF of \(Y\) given \(X\) is the joint PDF of \(X\) and \(Y\) divided by the marginal PDF of \(X\). It’s now clear why we discuss conditional distributions after discussing joint distributions: we need joint distributions to calculate the conditional distribution (the joint PDF is in the numerator!). Solution. Figure 5.8(a) shows $R_{XY}$ in the $x-y$ plane. The figure shows (a) $R_{XY}$ as well as (b) the integration region for finding $P(Y<2X^2)$ for Solved

R ∞ −∞ R ∞ −∞ f XY (x,y)dxdy= 1 Definition1.10(Marginaldistributions). LetXandY betwocontinuousrrvs on probability space (Ω,A,P) with joint pdf f XY.Then the pdf of X alone is calledthemarginal probability density function ofXandisdefinedby: f X(x) = Z ∞ −∞ f XY (x,y)dy, forx∈R (11) Similarly,thepdfofY aloneiscalledthemarginal probability density func- Problem calculating joint and marginal distribution of two uniform distributions. Ask Question Asked 8 years, 7 months ago. Active 1 year ago. what's the pdf and covariance for this distribution? 5. Problem obtaining a marginal from the joint distribution. 0.

4. Joint Distributions MATEMATIKA INTÉZET

SOA #92 Exam P Joint Uniform Distribution YouTube. That is, the conditional PDF of \(Y\) given \(X\) is the joint PDF of \(X\) and \(Y\) divided by the marginal PDF of \(X\). It’s now clear why we discuss conditional distributions after discussing joint distributions: we need joint distributions to calculate the conditional distribution (the joint PDF is in the numerator!)., That is, the conditional PDF of \(Y\) given \(X\) is the joint PDF of \(X\) and \(Y\) divided by the marginal PDF of \(X\). It’s now clear why we discuss conditional distributions after discussing joint distributions: we need joint distributions to calculate the conditional distribution (the joint PDF is in the numerator!)..

Joint density problem. Two uniform distributions

pdf Problem calculating joint and marginal distribution. 1 Order Statistics Definition The order statistics of a random sample X1, (Uniform order statistics pdf) The joint pdf of three or more order statistics could be derived using similar but even more involved arguments. Perhaps the other most useful pdf is fX (1),, 11/14/2015 · MathsResource.wordpress.com. Cumulative Distribution Function (CDF) and Properties of CDF/ Random Variables and Sample Space - Duration: 15:55. Engineering Made Easy 41,780 views.

and pdf is . Then the pdf of Proof: Let Y be a random variable that counts the number of less than or equal to x. Then we have ( ). Thus: ∑ 5. The Joint Distribution of Two Order Statistics Let denote the order statistics of a random sample, , from a continuous population with cdf and pdf . Then the joint pdf of 4. Joint Distributions Basic Theory Thus, by definition, the joint probability density function of (X, Y) is The following exercise shows how an arbitrary continuous distribution can be obtained from a uniform distribution. This result is useful for simulating certain continuous distributions.

Problem calculating joint and marginal distribution of two uniform distributions. Ask Question Asked 8 years, 7 months ago. Active 1 year ago. what's the pdf and covariance for this distribution? 5. Problem obtaining a marginal from the joint distribution. 0. If I'm understanding the question properly, we want to calculate the pdf of a multivariate uniform distribution. By definition, the pdf is constant for all values in the support the distribution. Thus to calculate the pdf all that is required is to calculate the norming constant, which is given by the inverse of the integral of the support.

6.1 Joint density functions Recall that X is continuous if there is a function f(x) (the density) such that P(X ≤ t) = Z t −∞ fX(x)dx We generalize this to two random variables. Definition 1. Two random variables X and Y are jointly continuous if there is a function fX,Y (x,y) on R2, called the joint probability density function… Lecture 10: Joint Distributions & Order Statistics Sta 111 Colin Rundel May 28, 2014 Joint Distributions Discrete RVs Joint Distribution - Example Draw two socks at random, without replacement, from a drawer full of twelve colored socks: 6 black, 4 white, 2 purple Let B …

6.1 Joint density functions Recall that X is continuous if there is a function f(x) (the density) such that P(X ≤ t) = Z t −∞ fX(x)dx We generalize this to two random variables. Definition 1. Two random variables X and Y are jointly continuous if there is a function fX,Y (x,y) on R2, called the joint probability density function… Theorem The difference of two independent standard uniform random variables has the standard trianglular distribution. Proof Let X1 and X2 be independent U(0,1) random variables. Let Y = X1 −X2. The joint probability density function of X1 and X2 is f X1,X2(x1,x2) = 1 0

Dall’Aglio G. (1997) Joint Distribution of Two Uniform Random Variables When the Sum and the Difference are Independent. In: Beneš V., Štěpán J. (eds) Distributions with … of the variables, the joint pmf or pdf of the subset is equal to the product of the marginal pmf’s or pdf’s. 12, ,..., ii i n XX X Slide 12 Stat 110A, UCLA, Ivo Dinov Conditional Probability Function Let X and Y be two continuous rv’s with joint pdf f (x, y) and marginal X pdf f X (x). Then for any X …

Bivariate Distributions — Continuous Random Variables When there are two continuous random variables, the equivalent of the two-dimensional array is a region of the x–y (cartesian) plane. Above the plane, over the region of interest, is a surface which represents the probability density function associated with a bivariate distribution. 4. Joint Distributions Basic Theory Thus, by definition, the joint probability density function of (X, Y) is The following exercise shows how an arbitrary continuous distribution can be obtained from a uniform distribution. This result is useful for simulating certain continuous distributions.

• A model for the joint distribution of age and length in a population of flsh can be used to estimate the age distribution from the length dis-tribution. The age distribution is relevant to the setting of reasonable harvesting policies. 1 Joint Distribution The joint behavior of … The converse does not hold in general. The joint distribution contains much more information than the marginal distributions separately. However, the converse does hold if \(X\) and \(Y\) are independent, as we will show below.. Joint and Marginal Densities

If I'm understanding the question properly, we want to calculate the pdf of a multivariate uniform distribution. By definition, the pdf is constant for all values in the support the distribution. Thus to calculate the pdf all that is required is to calculate the norming constant, which is given by the inverse of the integral of the support. Schaum's Outline of Probability and Statistics 36 CHAPTER 2 Random Variables and Probability Distributions (b) The graph of F(x) is shown in Fig. 2-1. The following things about the above distribution function, which are true in general, should be noted.

Problem calculating joint and marginal distribution of two uniform distributions. Ask Question Asked 8 years, 7 months ago. Active 1 year ago. what's the pdf and covariance for this distribution? 5. Problem obtaining a marginal from the joint distribution. 0. Problem calculating joint and marginal distribution of two uniform distributions. Ask Question Asked 8 years, 7 months ago. Active 1 year ago. what's the pdf and covariance for this distribution? 5. Problem obtaining a marginal from the joint distribution. 0.

The converse does not hold in general. The joint distribution contains much more information than the marginal distributions separately. However, the converse does hold if \(X\) and \(Y\) are independent, as we will show below.. Joint and Marginal Densities 1/29/2017В В· Learn to use pictures to solve problems involving Joint Uniform distributions. Joint Uniform Distribution Mancinelli's Math Lab. Joint Probability Distributions for Continuous Random

10/16/2015 · The distribution of the pipe length, however, is actually Uniform on the interval 10 feet to 10.57 feet. Assume that the lengths of individual pipes produced by the process are independent. Let X and Y represent the lengths of two different pipes produced by the process. What is the joint pdf for X and Y? 2. Homework Equations 3. Lecture 10: Joint Distributions & Order Statistics Sta 111 Colin Rundel May 28, 2014 Joint Distributions Discrete RVs Joint Distribution - Example Draw two socks at random, without replacement, from a drawer full of twelve colored socks: 6 black, 4 white, 2 purple Let B …

Formal Modeling in Cognitive Science

Let X have a uniform distribution over (0 2) and the. The joint probability distribution can be expressed either in terms of a joint cumulative distribution function or in terms of a joint probability density function (in the case of continuous variables) or joint probability mass function (in the case of discrete variables)., and pdf is . Then the pdf of Proof: Let Y be a random variable that counts the number of less than or equal to x. Then we have ( ). Thus: ∑ 5. The Joint Distribution of Two Order Statistics Let denote the order statistics of a random sample, , from a continuous population with cdf and pdf . Then the joint pdf of.

SOA #92 Exam P Joint Uniform Distribution YouTube. An n-dimensional joint uniform distribution is defined as a distribution whose one-dimensional marginals are uniform on some interval I. This interval is taken to be [0,1] or, when more convenient [−1 2, 1 9 2]. The specification of joint uniform distributions, Transformations Involving Joint Distributions 12 Note that to use this theorem you need as many Y i ’s as X i as the determinant is only deflned for square matrices..

SOA #92 Exam P Joint Uniform Distribution YouTube

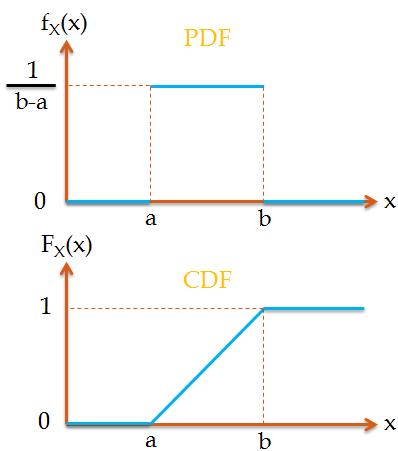
Sampling algorithms for generating joint uniform distributions. 6.1 Joint density functions Recall that X is continuous if there is a function f(x) (the density) such that P(X ≤ t) = Z t −∞ fX(x)dx We generalize this to two random variables. Definition 1. Two random variables X and Y are jointly continuous if there is a function fX,Y (x,y) on R2, called the joint probability density function… https://en.m.wikipedia.org/wiki/Discrete_uniform_distribution • A model for the joint distribution of age and length in a population of flsh can be used to estimate the age distribution from the length dis-tribution. The age distribution is relevant to the setting of reasonable harvesting policies. 1 Joint Distribution The joint behavior of ….

• A model for the joint distribution of age and length in a population of flsh can be used to estimate the age distribution from the length dis-tribution. The age distribution is relevant to the setting of reasonable harvesting policies. 1 Joint Distribution The joint behavior of … 6 Jointly continuous random variables Again, we deviate from the order in the book for this chapter, so the subsec-tions in this chapter do not correspond to those in the text. 6.1 Joint density functions Recall that X is continuous if there is a function f(x) (the density) such that P(X ≤ t) = Z t −∞ f X(x)dx

Problem calculating joint and marginal distribution of two uniform distributions. Ask Question Asked 8 years, 7 months ago. Active 1 year ago. what's the pdf and covariance for this distribution? 5. Problem obtaining a marginal from the joint distribution. 0. It is shown that, in a renewal process with inter-arrival distribution F, an observation from the asymptotic (when t в†’в€ћ) joint distribution of backward and forward recurrence times at t can be

Problem calculating joint and marginal distribution of two uniform distributions. Ask Question Asked 8 years, 7 months ago. Active 1 year ago. what's the pdf and covariance for this distribution? 5. Problem obtaining a marginal from the joint distribution. 0. Bivariate Distributions — Continuous Random Variables When there are two continuous random variables, the equivalent of the two-dimensional array is a region of the x–y (cartesian) plane. Above the plane, over the region of interest, is a surface which represents the probability density function associated with a bivariate distribution.

1 Order Statistics Definition The order statistics of a random sample X1, (Uniform order statistics pdf) The joint pdf of three or more order statistics could be derived using similar but even more involved arguments. Perhaps the other most useful pdf is fX (1), Schaum's Outline of Probability and Statistics 36 CHAPTER 2 Random Variables and Probability Distributions (b) The graph of F(x) is shown in Fig. 2-1. The following things about the above distribution function, which are true in general, should be noted.

It is shown that, in a renewal process with inter-arrival distribution F, an observation from the asymptotic (when t в†’в€ћ) joint distribution of backward and forward recurrence times at t can be The converse does not hold in general. The joint distribution contains much more information than the marginal distributions separately. However, the converse does hold if \(X\) and \(Y\) are independent, as we will show below.. Joint and Marginal Densities

Lecture 10: Joint Distributions & Order Statistics Sta 111 Colin Rundel May 28, 2014 Joint Distributions Discrete RVs Joint Distribution - Example Draw two socks at random, without replacement, from a drawer full of twelve colored socks: 6 black, 4 white, 2 purple Let B … Theorem The difference of two independent standard uniform random variables has the standard trianglular distribution. Proof Let X1 and X2 be independent U(0,1) random variables. Let Y = X1 −X2. The joint probability density function of X1 and X2 is f X1,X2(x1,x2) = 1 0

10/16/2015 · The distribution of the pipe length, however, is actually Uniform on the interval 10 feet to 10.57 feet. Assume that the lengths of individual pipes produced by the process are independent. Let X and Y represent the lengths of two different pipes produced by the process. What is the joint pdf for X and Y? 2. Homework Equations 3. An n-dimensional joint uniform distribution is defined as a distribution whose one-dimensional marginals are uniform on some interval I. This interval is taken to be [0,1] or, when more convenient [−1 2, 1 9 2]. The specification of joint uniform distributions

1.4 Conditional Distribution of Order Statistics In the following two theorems, we relate the conditional distribution of order statistics (con-ditioned on another order statistic) to the distribution of order statistics from a population whose distribution is a truncated form of the original population distribution function F(x). Theorem 2 Let and pdf is . Then the pdf of Proof: Let Y be a random variable that counts the number of less than or equal to x. Then we have ( ). Thus: ∑ 5. The Joint Distribution of Two Order Statistics Let denote the order statistics of a random sample, , from a continuous population with cdf and pdf . Then the joint pdf of

An n-dimensional joint uniform distribution is defined as a distribution whose one-dimensional marginals are uniform on some interval I. This interval is taken to be [0,1] or, when more convenient [−1 2, 1 9 2]. The specification of joint uniform distributions An n-dimensional joint uniform distribution is defined as a distribution whose one-dimensional marginals are uniform on some interval I. This interval is taken to be [0,1] or, when more convenient [−1 2, 1 9 2]. The specification of joint uniform distributions

Schaum's Outline of Probability and Statistics 36 CHAPTER 2 Random Variables and Probability Distributions (b) The graph of F(x) is shown in Fig. 2-1. The following things about the above distribution function, which are true in general, should be noted. In the case of the random sample of size 15 from the uniform distribution on (0;1), the pdf is f X(n)(x) = nx n 1 I (0;1)(x) which is the pdf of the Beta(n;1) distribution. Not surprisingly, all most of the probability or \mass" for the maximum is piled up near the right endpoint of 1. …

1.4 Conditional Distribution of Order Statistics In the following two theorems, we relate the conditional distribution of order statistics (con-ditioned on another order statistic) to the distribution of order statistics from a population whose distribution is a truncated form of the original population distribution function F(x). Theorem 2 Let In order to compare with the theoretical probability density function (PDF) , I need to simulate the probability density function of random variable. View How can I calculate the joint probability